SEG + DFS 응용법 and pro문제_디렉토리카운트
디렉토리카운트
최상위 디렉토리 7 보다 작은 하위 디렉토리의 개수 6
5보다 작은 디렉토리 개수 2
4보다 작은 디렉토리 개수 1
총합은 9
입력 ) 테스트 케이스 T
다음줄 디렉토리의 개수 N ,최상위 디렉토리의 수
다음줄 N-1개가 상위디렉토리 하위디렉토리 관계(상위 디렉토리 번호 , 하위 디렉토리 번호)
2 <= N <=3000
2
7 7 (7개의 디렉토리와 최상위 디렉토리는 7번노드이다.)
7 6
7 5
1 3
5 1
4 2
7 4
5 4
4 1
1 2
4 5
5 3
출력 예)
#1 9
#2 4
TC 1.

일단 이 문제가 좀 약점이 있다. DFS를 하려면 재귀를 돌려야 하는데 만약 1~2만개 정도의 편향된 그래프가 들어온다면
메모리 OUT이 걸리기 때문에 N의 개수가 좀 작다.
그래서 N이 3000이니깐 그냥 모든 노드에 대해서 DFS 때려서 구하면 되지 않나?????
이렇게 말이다. 어차피 3000x3000 걸릴턴데....
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
import java.util.*;
import java.io.*;
import java.math.*;
public class D210421_pro190615_디렉토리카운트_brute {
static int sum = 0;
static ArrayList<ArrayList<Integer>> edge;
public static void main(String[] args) throws IOException {
System.setIn(new FileInputStream("input2.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int tc = Integer.parseInt(br.readLine());
for(int z = 1 ; z <= tc ;z++) {
//long beforeTime = System.currentTimeMillis();
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int root = Integer.parseInt(st.nextToken());
sum = 0;
edge = new ArrayList<ArrayList<Integer>>(n+1);
for(int i = 0 ; i <= n; i++)
edge.add(new ArrayList<Integer>());
for(int i = 0 ; i < n-1 ; i++) {
st = new StringTokenizer(br.readLine());
int ss = Integer.parseInt(st.nextToken());
int ee = Integer.parseInt(st.nextToken());
edge.get(ss).add(ee);
}
for(int i = 1 ; i <= n ; i++)
go(i, i);
//long afterTime = System.currentTimeMillis();
//System.out.println("#"+z+" "+sum + " " +(afterTime-beforeTime));
}
}
static void go(int base, int cur_node) {
//System.out.println(base+ " " + cur_node);
if(base > cur_node)
sum++;
int size = edge.get(cur_node).size();
for(int i = 0 ; i < size ; i++)
go(base, edge.get(cur_node).get(i));
}
}
|
cs |
이렇게 말이다.
근데 프로문제가 이렇게 간단하게 나올리는 없고 이 문제가 무엇을 원하는가를 찾아보는데 중점을 두었다.
아무튼 그러면 만들어진 전체 그래프를 기준으로 어떻게 하면
각 탐색마다 N이 아닌 log2N 을 해줄 수 있는지 고민해야 한다.
루트노드는 주어졌으니 그래프 그리는건 어렵지 않고 음........
여기서 이것을 볼 수 있어야 한다. 일단 그래프 하나 그려보자.

직관적으로 보면 이게 당연한 거지만 내가 만일 DFS로 4번노드(끝)까지 탐색했었을 때 이렇게 연결 되어있는 것으로
4 보다 작은 하위 디렉토리의 개수를 어떻게 짤 것인가???
0개인것 알겠는데 말이야......
그것보다 더 잘 봐야 하는것은
그리고 6번 탐색을 끝내고 5번으로 되돌아 왔을 때 이것이 하위 디렉토리 수가 1개인건 어떻게 알 수 있을까?
저장된 노드라면 1,3,2,6,5 가 있고 하위 디렉토리를 알려면 4를 알아야 하는데.... 모른단 말이야.....
5번노드에서 또 DFS식 탐색???? 그러면 O(N)인데?????
이 아이디어를 잡아야 한다.
상위 디렉토리 V1 보다 작은 하위 디렉토리의 개수 N개 는
---->
하위 디렉토리 V2 보다 큰 상위 디렉토리의 개수 N개 (크거나 같다 해봤자 어차피 같은 번호의 노드는 없을꺼니 pass)
이렇게 바꿀 수 있어야 한다.!!!!!!!!!
잠시만 수학적 역으로는 맞는 말이긴 하지만 이게 진짜 된다고??????
해보자

어??????? 답이 같네?????
일단 로직을 생각해 보자.
4번노드 탐색 시 4번노드보다 큰 상위 디렉토리 수 를 구한다면 밑으로 내려오면서
1 3 2 6 5 4 를 어디다가 저장해놨을터니깐 이 저장한 것들중에서 4보다 큰건 5,6이니깐 답은 2개 라는건 알겟는데......
1 3 2 6 5 4 여기서 5,6을 그냥 뽑을라면 N만큼 또 탐색해야 하자나???
여기서 필요한게 세그먼트 트리이다.
세그먼트는 수의 추가, 원하는 수의 추출 둘다 log2N이 걸린다.
세그먼트 트리의 원리는 검색하면 널려있으니깐 찾아서 일단 보면 되고......
아무튼 저 1 3 2 6 5 4 를 세그를 통해서 해보자
일단 1 3 2 6 5 4 DFS탐색하면서 update 해보자.
일단 최하위 노드인 4번까지 오면 세그트리는 이런 상태일 것이다.
여기서 1~6을 가리키는 노드는 현재 탐색되어진 1~6번 노드의 개수의 합이다.

좀 이해가 안가는가???? 그러면 문제의 노드 기준으로 다시 한번 설명한다.
그러면 이 노드 기준으로 DFS 탐색을 으로 3번노드에 도착해왔다라는건
7,5,1,3번노드를 품고 있는 상태이므로 (4,2는 DFS 재귀로부터 빠져나왔지 않았는가)
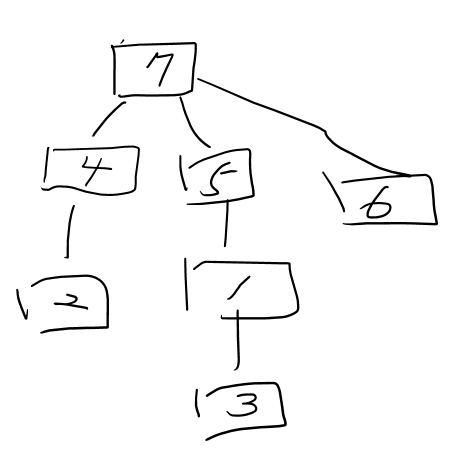

이런 세그트리 상태일 것이다.
그러면 4번노드 기준
하위 디렉토리 V2 보다 큰 상위 디렉토리의 개수 N개 (크거나 같다 해봤자 어차피 같은 번호의 노드는 없을꺼니 pass)
이것을 생각하면
5번노드 ~6번노드가 품고 있는 수(sum) 을 찾으면 될것이 아닌가? 그러면 2가 나올 것이다.

이렇게 말이다
이제 4번노드를 빠져나오고 5번트리 로 되돌아 오면 이 세그트리에서
update(4번트리 , -1)을 해주니깐

이런 상태일 것이고 5번노드 기준
6번노드 ~6번노드가 품고 있는 수(sum) 을 찾으면 될것이 아닌가? 그러면 1이 나올 것이다.
이것을 이렇게 풀면 된다.
여기서 sum이나 update나 세그먼트 트리 특성상 전부 log2N의 시간이 걸린다.
그러면 이제 이것을 짜주면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
import java.util.*;
import java.io.*;
import java.math.*;
public class D210421_pro190615_디렉토리카운트_seg {
static ArrayList<ArrayList<Integer>> edge;
static int v;
static int root;
static int[] segarr;
static int[] cnt;
static int ans;
public static void main(String[] args) throws IOException {
//System.setIn(new FileInputStream("input2.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int tc = Integer.parseInt(br.readLine().trim());
for(int z = 1 ; z <= tc ; z++) {
StringTokenizer st = new StringTokenizer(br.readLine());
v = Integer.parseInt(st.nextToken());
root = Integer.parseInt(st.nextToken());
segarr = new int[v*4];
cnt = new int[v+1];
ans = 0;
edge = new ArrayList<ArrayList<Integer>>();
for(int i = 0 ; i <= v ; i++)
edge.add(new ArrayList<Integer>());
for(int i = 1 ; i < v ; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
edge.get(s).add(e);
}
init(root);
System.out.println("#"+z+" " +ans);
}
}
static void update(int node, int start, int end, int target, int diff) {
if(target < start || end < target)
return;
segarr[node] += diff;
if(start == end)
return;
int mid = (start+end)/2;
update(node*2, start, mid , target, diff);
update(node*2+1, mid+1, end, target, diff);
}
static int getSum(int node, int start, int end , int left , int right) {
if(end < left || right < start)
return 0;
if(left <= start && end <= right)
return segarr[node];
return getSum(node*2, start , (start+end)/2, left, right) + getSum(node*2+1, (start+end)/2+1 , end, left, right);
}
static void init(int cur_node) {
update(1,1,v,cur_node, 1);
int size = edge.get(cur_node).size();
for(int i = 0 ; i < size ; i++)
init(edge.get(cur_node).get(i));
update(1,1,v,cur_node, -1);
System.out.println(cur_node + " " + Arrays.toString(segarr));
ans += getSum(1, 1, v, cur_node, v);
}
}
|
cs |