다각형 내부, 외부 판별 + pro문제_말뚝 울타리 치기
일단 문제부터 보자.
□ 문제유형 : 말뚝 울타리 치기
[문제]
말뚝이 박혀 있는 땅에 울타리를 치려고 한다.
울타리는 가장 외곽에 있는 말뚝을 기준으로 칩니다.
이렇게 울타리를 완성했는데, 새로운 말뚝을 발견합니다.
만약 새로운 말뚝이 울타리 안에 있으면 상관없지만,
울타리 바깥에 있는 말뚝이라면 울타리를 새로 쳐야합니다.
울타리를 새로 쳐야 하는 말뚝의 갯수를 세는 프로그램을 작성하시오.
[입력조건]
최초로 테스트케이스 가 주어진다.
그 다음 말뚝의 갯수 N (3 ~ 1,000)
그 다음 N개의 x,y좌표 (x,y:0 ~ 10억)
그 다음 새로운 말뚝의 갯수 Q (1 ~ 100)
그 다음 Q개의 x,y좌표 (x,y:0 ~ 10억)
[출력조건]
Q개의 말뚝중에서 새로 울타리를 쳐야 하는 말뚝의 갯수
[제한사항]
java 1.5 초 이내
[입력 예]
2
10
1 1
5 10
11 8
8 6
3 4
2 0
10 10
5 5
4 5
9 7
3
2 8
11 11
4 2
3
0 8
8 0
8 8
1
5 5
[출력 예]
#1 2
#2 0
ㅈㄴ 딱봐도 컨벡스 헐헐헐 문제다.
여기서 새로운 말뚝을 박았을떄 말뚝이 기존 울타리 안에 있는지 바깥에 있는지 판별하는 문제이다.
기존 말뚝들의 다각형 만들기는 헐로 풀면 되는데 새로운 말뚝에 대한 판별을 어떻게 할까...............
짱구를 굴려보고 기존에 풀어봤었던 것들을 생각해보니깐
다각형의 내 외부 판별을 하면 되겠다!!! 라는 생각이 들었다.
그래서
[기하] 다각형의 내부 외부 판별
[기하]다각형의 내부 외부 판별 목차 [기하] 다각형의 내부 외부 판별 다각형의 내부 외부 판별이란? 아이디어 다각형의 내부에 위치하는 점의 특징은 뭘까? 구현 어떻게 반 직선과 다각형의 교
bowbowbow.tistory.com
이것을 열심히 읽어보았다.
그래서 이 글의 핵심 요약은
다각형이 있을때 각 선분과 특정 점 B에 대해서 각각
- 점B의 y좌표가 두 선분 꼭지점의 y좌표 사이에 있다.
- 점B를 지나는 수평선과 선분 사이의 교점의 x좌표가 점B의 x좌표보다 크다.
이것을 만족하면 된다.
즉 이렇게 하면 만족한다는 뜻이다.

이것을 만족시킬때 마다 cnt++ 를 하고
모든 선분을 탐색하고
cnt가 홀수이면 다각형의 안쪽
짝수이면 다각형의 바깥쪽 이다.
주의점 1.
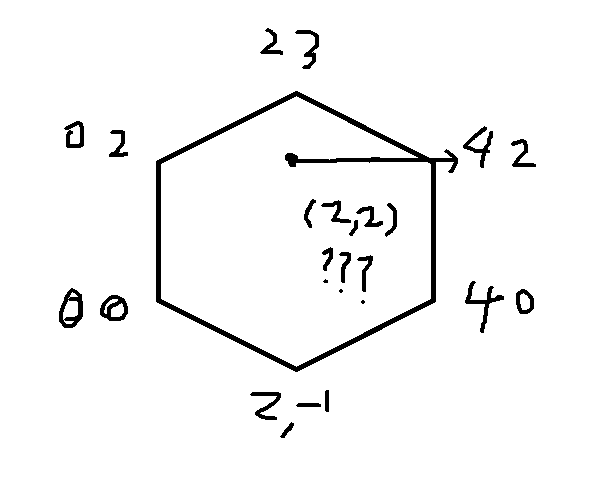
요런 정육각형과 좌표가 주어지고 (2,2) 에 대한 내외부 판별을 해보자.
그러면
(4,0),(4,2) 에 대한 직선이 조건에 만족하지 않고
(4,2),(2,3)에 대한 직선이 조건에 만족하지 않으니깐
cnt는 0가 나와서 다각형의 바깥이다 라는 값이 나오지만 그림과 같이 안에 있다.
즉, 반직선을 그었을때 선분의 끄트머리에 걸치면 2개의 값이 중복이 되면서 오류가 터진다는 것이다.
이것을 어떻게 해결할까???
답은 :
- 점B의 y좌표가 두 선분 꼭지점의 y좌표 사이에 있다.
이것을 잘 조절 해보면 된다.
두 선분을 (x1, y1) , (x2, y2) 라고 하고 점 B의 좌표는 (a,b) 라고 해보자.
그러면 기존에는 그냥 사이라고 했으니깐
점B의 y좌표가 두 선분 꼭지점의 y좌표 사이에 있다. 라는 조건을
if(y1 < b && b < y2 || y2 < b && b <y1) // 미만~ 미만
이렇게 적었을 것이다.
이것을 이렇게 말고
if((y1 <= b && b < y2) || (y2 <= b && b < y1)) // 이상 ~ 미만
이렇게 하면 위에 "2개의 값이 중복이 되면서 오류가 터진다는 것이다." 라는 것이
1개만 값이 들어오기 때문에 이 오류를 피할 수 있지 않겠는가???
직접 해보자.

이 그림에서 문제가 있는 선분을 잡아보자.
(4,0) ~ (4,2) 와 (4,2) ~ (2,3) 이 두 선분이다.
그리고 "점B를 지나는 수평선과 선분 사이의 교점의 x좌표가 점B의 x좌표보다 크다."
이 조건은 둘다 성립하니깐 일단 생략하겠다.
선분 [(4,0), (4,2)] 와 점 (2,2) 에 대해서 조건을 잡아보자.
if((y1 <= b && b < y2) || (y2 <= b && b < y1))
==
if( (0 <= 2 && 2 < 2) || (2 <= 2 && 2 < 0) )
false false => 조건 만족 실패
선분 [(4,2), (2,3)] 와 점 (2,2) 에 대해서 조건을 잡아보자.
f((y1 <= b && b < y2) || (y2 <= b && b < y1))
==
if( (2 <= 2 && 2 < 3) || (3 <= 2 && 2 < 2) )
true false => 조건 만족
이렇게 해서 두 선분이 겹치는 지점에 반직선이 지나도 둘중 하나만 만족하도록 공식을 개선할 수 있다.
주의점2.
만약 말뚝이 이렇게 박혀있으면 어떻게 하나????

그래도 이건 방법이 좀 쉽다.
선분과 점에 대한 다각형의 내부 외부 판별 하다가
- 점B를 지나는 수평선과 선분 사이의 교점의 x좌표가 점B의 x좌표보다 크다.
이 조건이
점 B를 지나는 수평선과 선분 사이의 교점의 x좌표가 점 B의 좌표와 같다면??????
위 그림과 같은 형태가 되어 버린다는 것이 아니겠나??
그러면 이것은 (4,1) 말뚝이 내외부 판별용 cnt 갯수와 관계없이 울타리를 새로 치지 않아도 되기에
(어차피 기존 울타리와 겹쳐져 있으니 굳이 칠 필요는 없다.)
탐색을 중단하고 이 울타리는 새로 안쳐도 된다는 결론이 나온다.
주의점 3
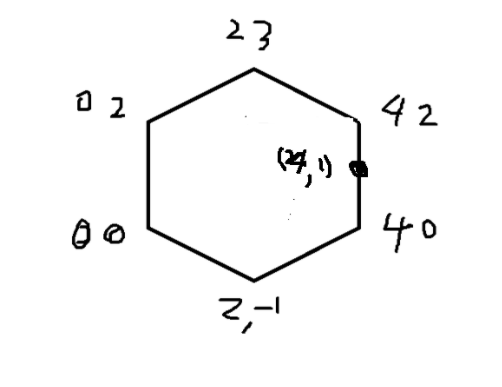
(0,0), (2,-1), (4,0) (4,2) (2,3) (0,2) 에 대해서 선분 탐색을 할때
(2,3) (0,2) 선분 -> (0,2), (0,0) 선분도 탐색해야 한다. 자칫하면 놓친다.....
이걸 기반으로 코드를 구현했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
|
import java.util.*;
import java.io.*;
import java.math.*;
public class D210420_pro181110_말뚝울타리치기 {
//first = y좌표가 가장 작은 점이나 x좌표값이 가장 작은 점을 기준점으로 잡음
static Point first;
public static void main(String[] args) throws IOException {
System.setIn(new FileInputStream("input2.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int tc = Integer.parseInt(br.readLine());
for(int z = 1 ; z <= tc ; z++) {
ArrayList<Point> arr = new ArrayList<Point>();
ArrayList<Point> q_arr = new ArrayList<Point>();
int n = Integer.parseInt(br.readLine());
for(int i = 0 ; i < n ; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
arr.add(new Point(x, y));
}
int q = Integer.parseInt(br.readLine());
for(int i = 0 ; i < q ; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
q_arr.add(new Point(x, y));
}
first = new Point(Long.MAX_VALUE, Long.MAX_VALUE);
for(int i = 0 ; i < arr.size(); i++) {
if(arr.get(i).y < first.y)
first = arr.get(i);
else if(arr.get(i).y == first.y && arr.get(i).x < first.x)
first = arr.get(i);
}
//기준점과 나머지점들이 ccw로 반시계방향(좌회전)이 되도록 정렬을 시키고, 만약 일직선상에 있으면 거리가 증가하게끔 정렬을 시킴
Collections.sort(arr, new Comparator<Point>() {
@Override
public int compare(Point second, Point third) {
int ccw_Result = ccw(first, second, third);
if(ccw_Result > 0)
return -1;
else if(ccw_Result < 0)
return 1;
else{
long dist1 = dist(first, second);
long dist2 = dist(first, third);
return Long.compare(dist1, dist2);
}
}
});
//ArrayList 그라함 스캔 start
ArrayList<Point> s= new ArrayList<Point>();
s.add(first);
for(int i = 1 ; i < arr.size(); i++) {
//스택의 마지막-1 == a, 스태의 마지막 == b, 잡을 점 == P 일때 ccw(a,b,P) 가 > 0 이여야 스택에 넣어야 한다.
while(s.size() >= 2 && ccw(s.get(s.size()-2), s.get(s.size()-1), arr.get(i)) <= 0)
s.remove(s.size()-1);
s.add(arr.get(i));
}
// 여기까지는 https://jaeyoon8783.tistory.com/82 코드와 거의 같다.
/*
for(int i = 0 ; i < s.size() ; i++)
System.out.println(s.get(i).x + " " + s.get(i).y);
*/
/*
cnt++ 조건
점B의 y좌표가 두 선분 꼭지점의 y좌표 사이에 있다.
점B를 지나는 수평선과 선분 사이의 교점의 x좌표가 점B의 x좌표보다 크다.
이 cnt가 홀수이면 안, 짝수면 바깥
조건 중에 만약 점B가 선분과 겹쳐 있다? 그 말뚝은 뭐가 어쨋든 추가 말뚝이 아니니깐 바로 끝낸다.
*/
int ans = 0;
for(int i = 0 ; i< q_arr.size(); i++) {
Point tp = q_arr.get(i);
int cnt = 0;
boolean flag = true;
for(int j = 0 ; j < s.size() ; j++) {
Point pa = s.get(j);
Point pb = s.get((j+1)%s.size()); // 주의점 3에 해당
/* 선분의 방정식
(y - pb.y) = (pb.y-pa.y) * (x - pb.x) /(pb.x-pa.x)
y = tp.y
(tp.y - pb.y) = (pb.y-pa.y) * (x - pb.x) /(pb.x-pa.x)
(tp.y - pb.y) * (pb.x-pa.x) / (pb.y-pa.y) = x - pb.x
x = (tp.y - pb.y) * (pb.x-pa.x) / (pb.y-pa.y) + pb.x;
*/
//점B의 y좌표가 두 선분 꼭지점의 y좌표 사이에 있다.
//if((pa.y < pb.y && pa.y < tp.y && tp.y < pb.y) || (pa.y > pb.y && pb.y < tp.y && tp.y < pa.y)) { // 주의점 1에 해당. 이코드를 밑에와 같이
if((pa.y <= tp.y && tp.y < pb.y) || (pb.y <= tp.y && tp.y < pa.y)) {
long tmp_x = (tp.y - pb.y) * (pb.x-pa.x) / (pb.y-pa.y) + pb.x;
if(tp.x < tmp_x)
cnt++;
else if(tp.x == tmp_x) { // 주의점 2에 해당
flag = false;
break;
}
}
}
//System.out.println(tp.toString() + " " + flag + " " + cnt);
if(flag == true && cnt %2 == 0 )
ans++;
}
System.out.println("#"+z+" " +ans);
}
}
static class Point {
long x;
long y;
Point(long x, long y) {
this.x = x;
this.y = y;
}
public String toString() {
return "["+x + ", " + y + "]";
}
}
static int ccw(Point a , Point b , Point c) {
long n = (a.x * b.y + b.x * c.y + c.x * a.y) - (b.x * a.y + c.x * b.y + a.x * c.y);
if (n > 0)
return 1;
else if (n < 0)
return -1;
else
return 0;
}
static long dist(Point a, Point b) {
return (b.x - a.x) * (b.x - a.x) + (b.y - a.y) * (b.y - a.y);
}
}
|
cs |
정보 - Color Scripter
Simple & Flexible Syntax HighLighter
colorscripter.com
그런데.... 문제는
강사님의 모범답안을 보고 오니깐 더 쉽게 푸는 방법이 있었다;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
그냥 기존말뚝, 새말뚝 다 때려놓고
컨벡스 헐 만든 다음에
만들어진 다각형에서 새말뚝이 있나 를 찾으면 되는 것이였다;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
이건 나중에.....